이번에는 꽤나 재미있는 작업을 해 볼 것이다.
물체의 표면에서 나오는 벡터를 나타내는 VertexNormal을 내적(Dot)을 하여 경사로의 알파값으로 이용할 것이다.

우선 경사로의 돌은 보다 텍스처 크기를 크게 쪼개야하므로 따로 파라미터로 지정한다.

위와 같이 강도를 낮추면 보다 큰 돌질감이 나타난다.

다음으로 VertexNormal의 내적이다.
수학이 조금 들어가서 어려울 수 있는데 내적의 원리만 알면 간단하다.

a 벡터와 b 벡터의 내적은 |a| x |b| x cos θ로 표현이 되는데 코사인의 값에 따라 직각일 경우 0, 평행일 경우 1 이며 그 사이의 경우 0~1 사이의 값이 된다.
이를 이용하면 특정한 벡터와 물체의 표면 벡터들을 내적하였을때 값들이 0~1 사이로 분포하고 이를 활용할 수 있다.

위는 언리얼 홈페이지에서 내적(Dot) 함수의 설명을 가져온 것이다.
잘 보면 물체의 VertexNormal 값과 사용자가 바라보는 카메라의 내적을 구해서 그 값을 활용한 예시이다.
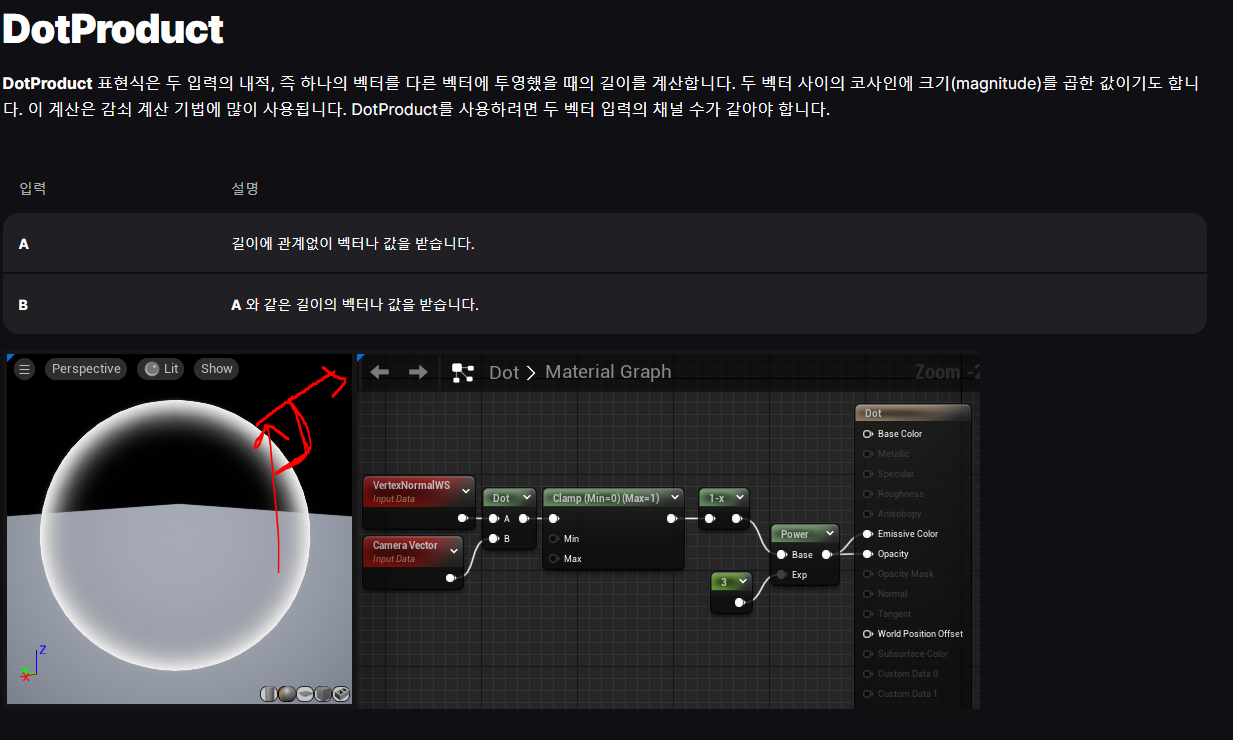
물체의 외각일수록 카메라의 각도와 수직에 가까워 내적값이 0으로 수렴한다. (코사인 90도 값이 0이므로)
이를 1- 함수로 반전시켜 외각일수록 1에 가까이, 중앙일수록 0에 가까이 만들고 Power(제곱)함수로 이 값을 증폭시켜 물체의 Emissive와 Opacity에 연결하여 외각일수록 빛을 발하고 불투명도를 높이고 중앙일수록 빛을 발하지 않고 불투명도를 낮춰 투명하게 한 예시이다.
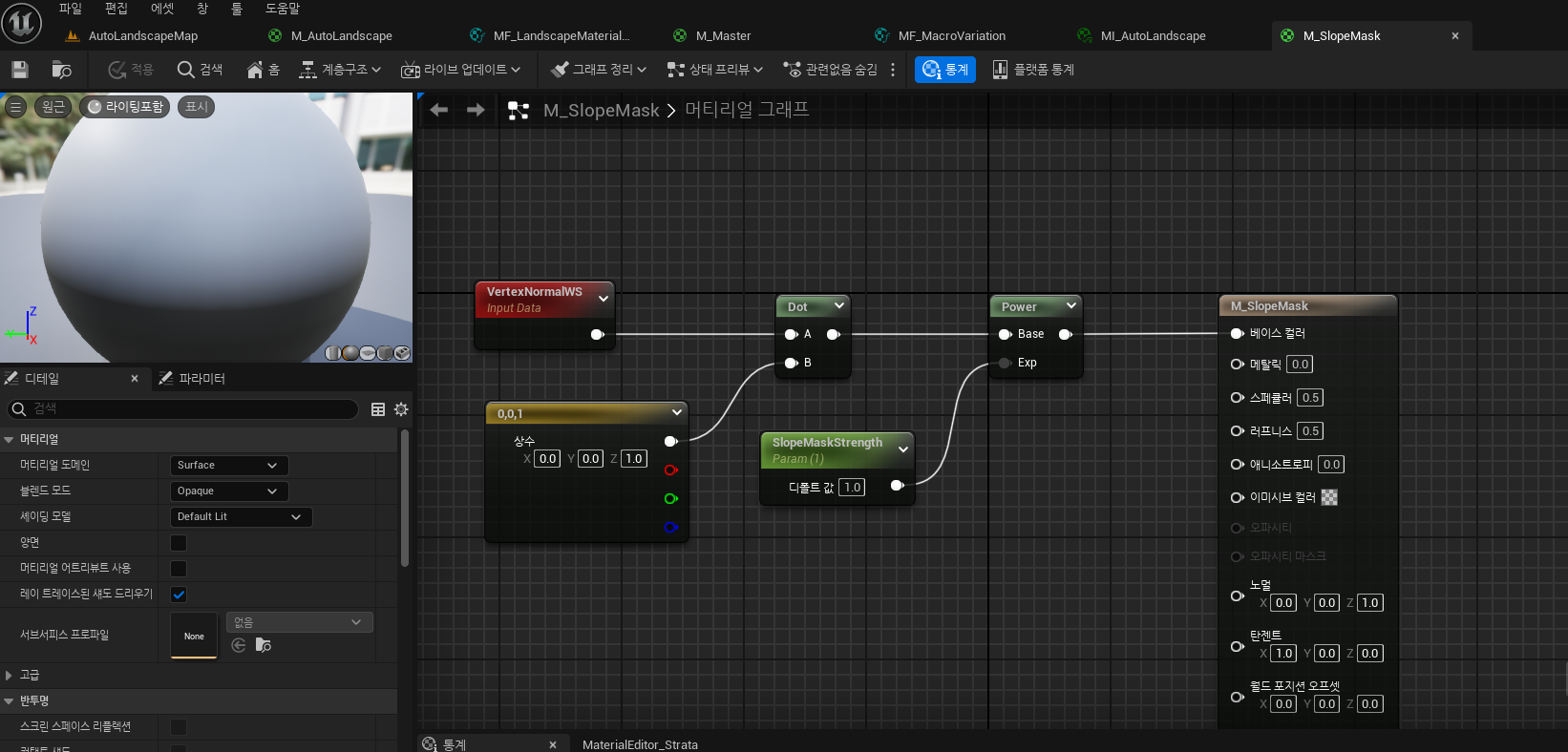
다시 예시로 만든 머티리얼을 보면 예시와 비슷하게 물체의 VertexNormal 값들과 Z방향 위를 향하는 {0, 0, 1} 벡터를 내적시켜 값을 구하고 제곱으로 증폭시킨다.
이러면 평면일수록 VertextNormal 벡터가 {0, 0, 1} 벡터와 평행이되어 1에 가까워지고 경사가 심할수록 0에 가까워진다.

이를 땅에 적용시켜보면 위와 같이 평면일수록 1에 가까워 흰색을, 경사가 심할수록 0에 가까워 검은색을 띈다.

우리가 필요한건 반대이므로 1-함수로 반전시키고 Saturate 함수로 0~1값으로 고정한다.

반전시키면 위와 같이 나타난다.

이것을 토대로 머티리얼 함수를 만든다.

이 머티리얼 함수를 바탕으로 블렌드를 해 준다.
그럼 두 머티리얼이 만나는 곳은 0~1값을 가지게 되어 보다 자연스럽게 블렌드가 될 것이다.

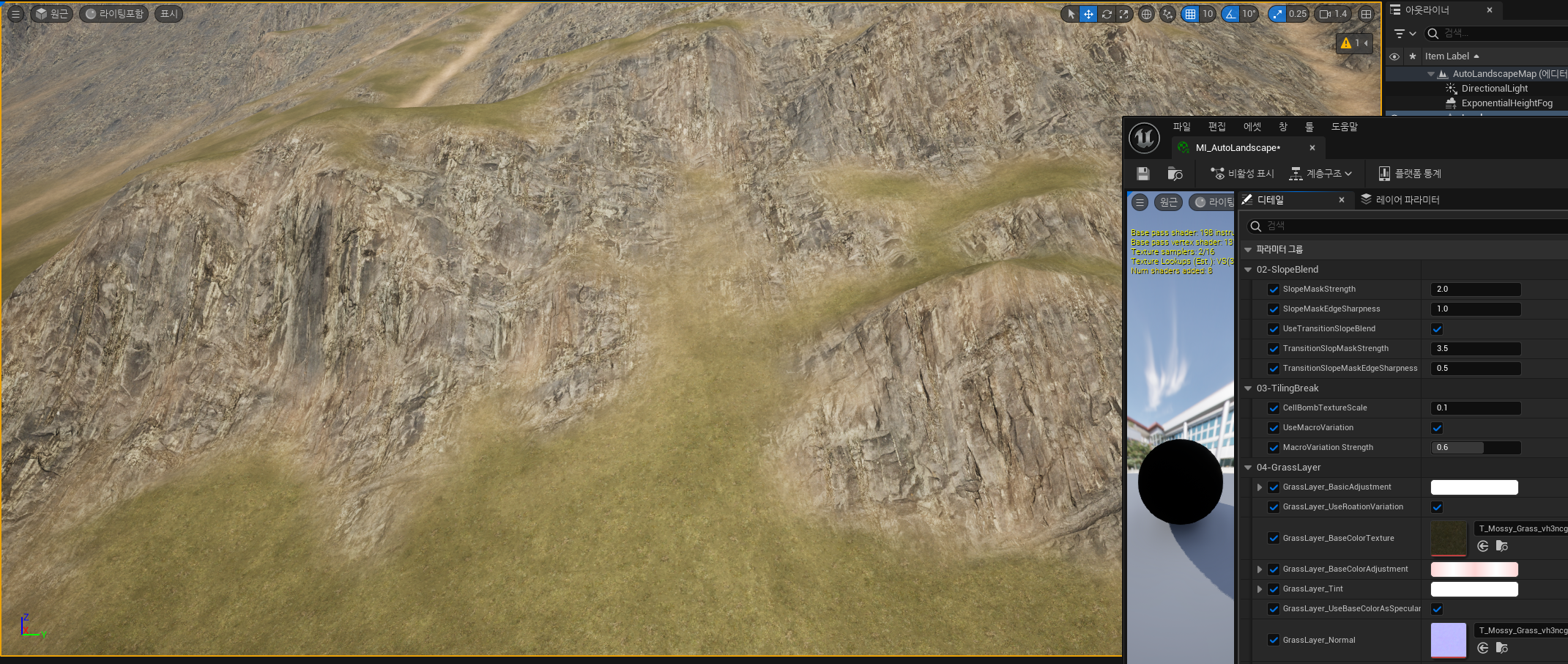
위와 같이 적용전과 비교하였을 때 만나는 부분이 더 자연스럽게 변하는 효과를 볼 수 있다.
'언리얼 - Material' 카테고리의 다른 글
| Material (8) _ Triplanar (0) | 2024.07.13 |
|---|---|
| Material (6) _ 랜드스케이프 블렌드 (1) | 2024.07.12 |
| Material (5) _ Specular, Normal, ORD 추가 (0) | 2024.07.11 |
| Material (4) _ Landscape 지형생성 및 타일링 제거하기 (0) | 2024.07.10 |
| Material (3) _ 머터리얼 블렌드 및 시네마틱 카메라 (0) | 2024.07.10 |